Write your first question

In this tutorial you will learn about the structure and features of a Numbas question by creating a simple numeracy problem.

To begin, let’s make this question:

Chris eats 7 apples per day. How many apples does he eat per week?

Log in to the Numbas editor and, in the Create box, click on the Question link.

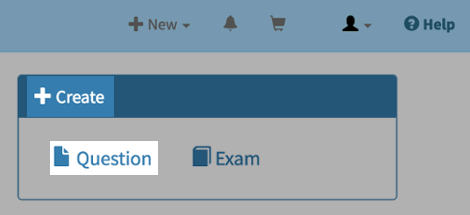
You will be prompted to give your question a name, and to assign it to a project. Call the question “Given a quantity per day, how many per week?” As this is your first question you should use the default project, which is your own workspace.

There are two modes for Numbas questions, determining how parts are presented to the student: Show all parts and Explore. For this question, use ‘Show all parts’.

Giving the question a name.

The structure of a question

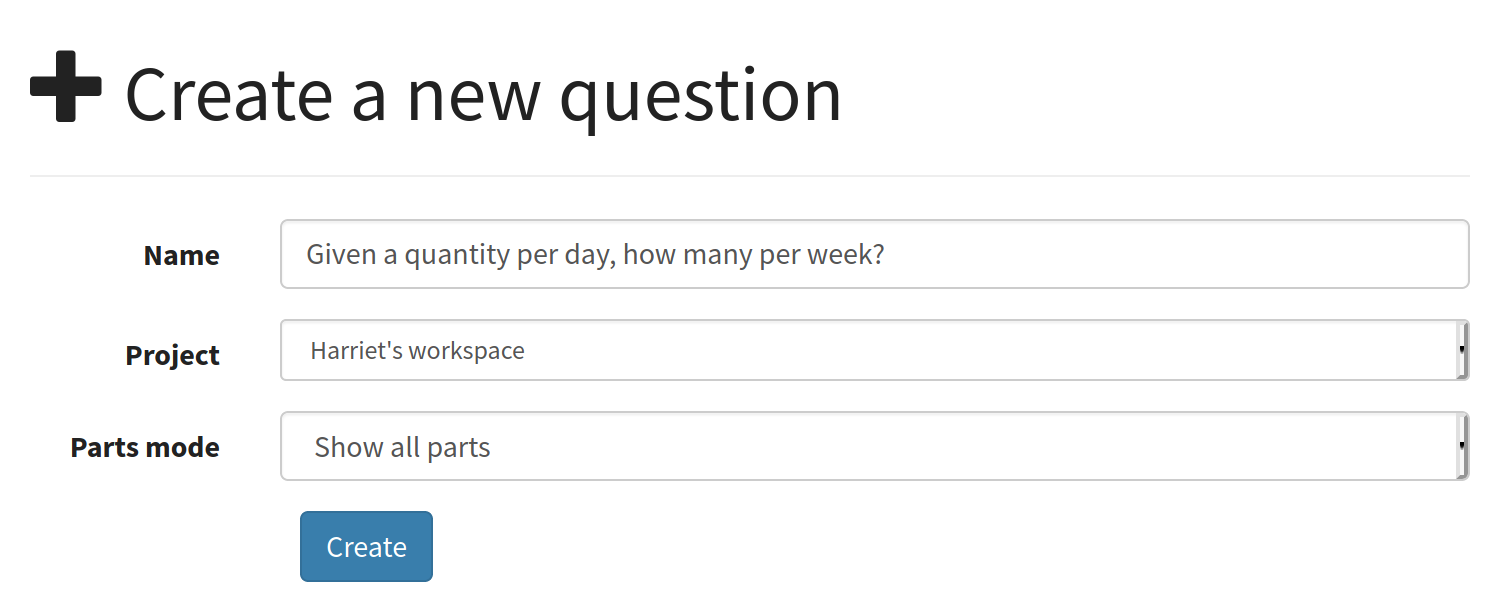
You are taken to the editing page for your new question. It is worth spending a few moments finding your way around this page.

At the top of the page are the question’s name and, above that, a link to the project which it belongs to. Below are buttons to run and download the question, along with options to navigate through the various steps involved in editing a question.

The question editor.

Beneath these is the main editing interface.

Every Numbas question consists of three sections: Statement, Parts, and Advice. In the Statement, the context for the question is given to the student. Parts are where the student enters their answers: the student is shown some prompt text, and then a field to enter their response to the prompt. A question can have one or more parts, each of which is one of several types, depending on what kind of input you want from the student. Finally, the optional Advice section can be used to give a full solution to the question, which the student can request to see if they’re stuck.

Each of these sections of the editor can be accessed from the links in the navigation bar, or you can use the buttons at the bottom of each section to guide you through in a logical order.

Planning

It’s important to plan your question before you start writing it.

In this question, we will assess whether the student can convert a quantity per day into a quantity per week.

They’ll be told how many apples a person eats per day, and then be asked to write down how many apples per week the person eats.

Their answer will be marked correct if it’s seven times the given number. One way of getting a wrong answer is to divide by seven instead of multiplying by seven.

A natural way to randomise the question is to randomise the number of apples eaten per day.

Statement

The statement sets the scene for the question, giving any necessary information. It’s a rich text editor, so in addition to text you can add video, images, anything you like here.

The statement is optional, and ours is going to be very short, but let’s go for it anyway.

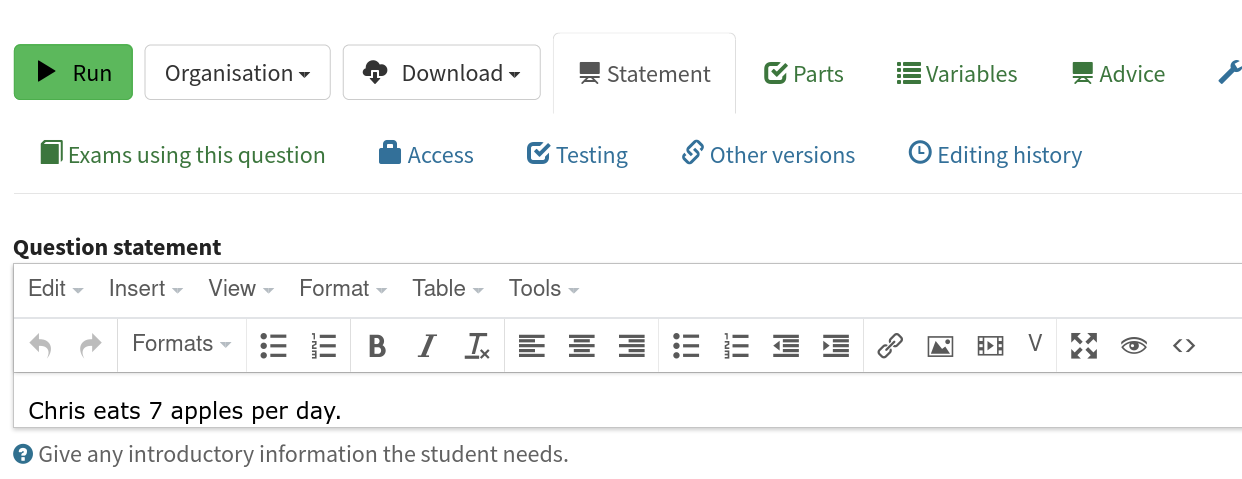
Type:

Chris eats 7 apples per day.

in the Question statement box.

Note

Rich text editors such as the question statement box initially display a rendering of their contents. Click on the box to start editing it.

Writing a question statement.

Notice that you can click Run to preview your question at any time. A new browser tab opens, showing the question as a student would see it. Switch back to the editor tab when you’re ready to make more changes.

Note

There’s no ‘Save’ button: the editor saves your changes automatically. At the top-right of the screen is a little box describing the status of your changes, either “Saved”, “Unsaved changes”, or “Saving”.

Parts

If you run the question now, you’ll see there is a statement, but no prompt to do anything and nowhere to enter an answer.

Let’s ask the student to work out how many apples Chris eats in a week.

Go back to the editing window and click on Parts in the navigation bar, or follow the navigation buttons at the bottom of the page.

You’re shown a list of part types. We want the student to give a number, so select Number entry.

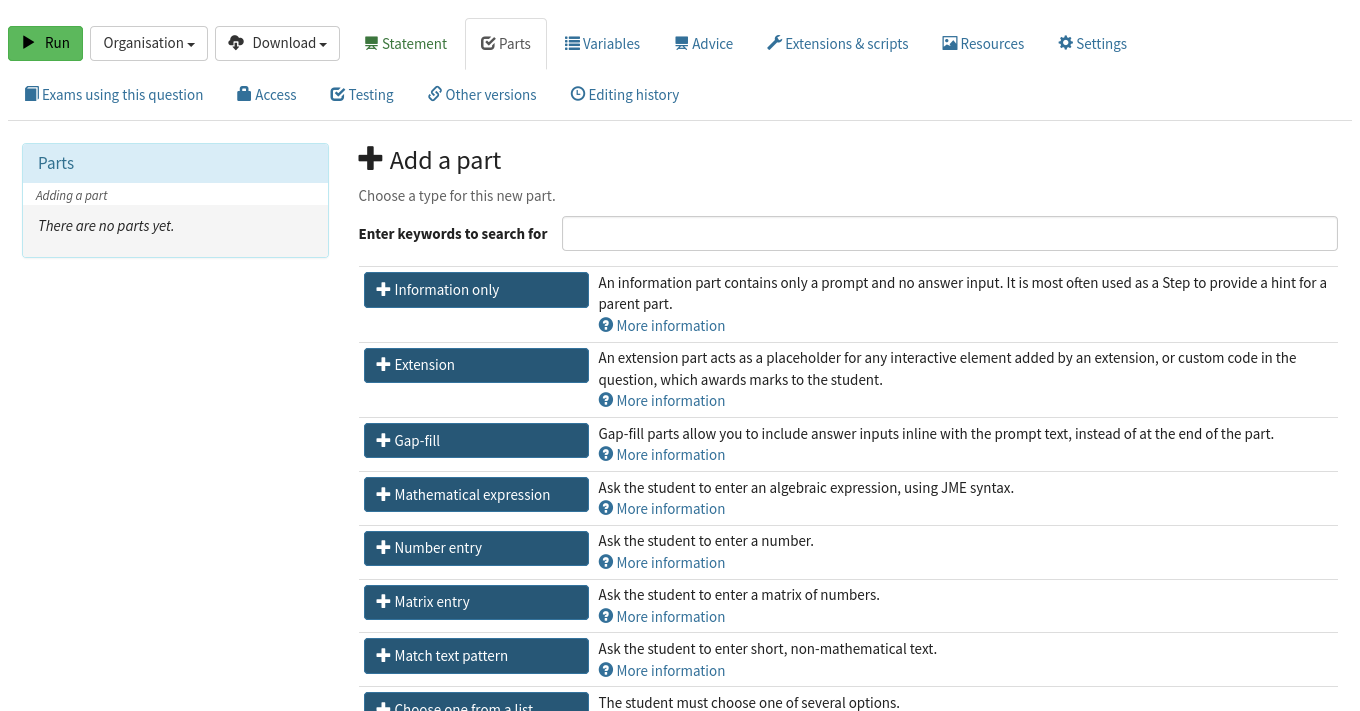
Selecting a part type.

Every part has a Prompt which you can use to tell the student how to answer the part.

Type:

How many apples does Chris eat per week?

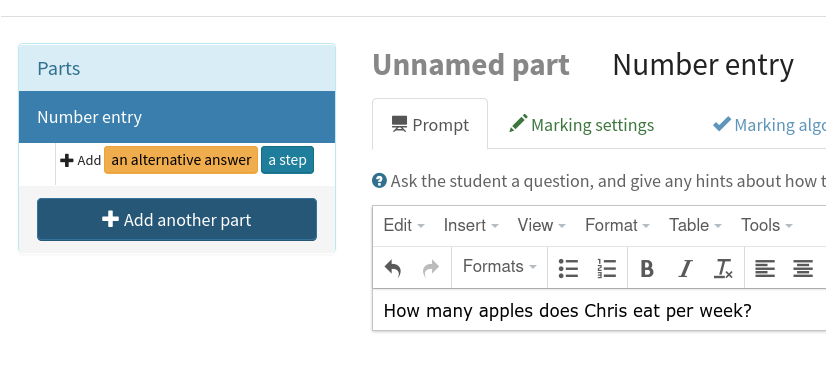
Filling in the prompt.

Now we need to specify the answer. Move to the Marking settings tab.

Number entry parts are marked by checking if the student’s answer is within the range defined by the Minimum accepted value and Maximum accepted value fields. For this question the answer is exactly \(49\), so put that in both fields.

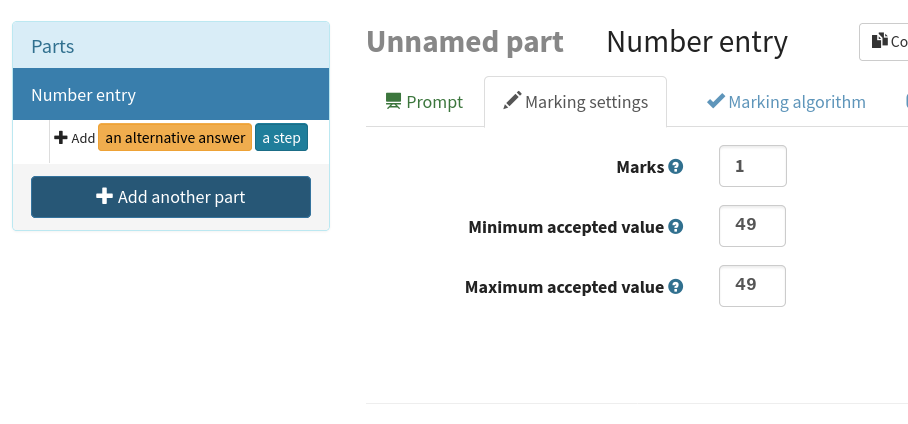
Specifying the correct answer.

Now press Run again to try out the question.

If you put 49 in the entry box and press Save answer, the answer is marked correct; any other number is marked incorrect.

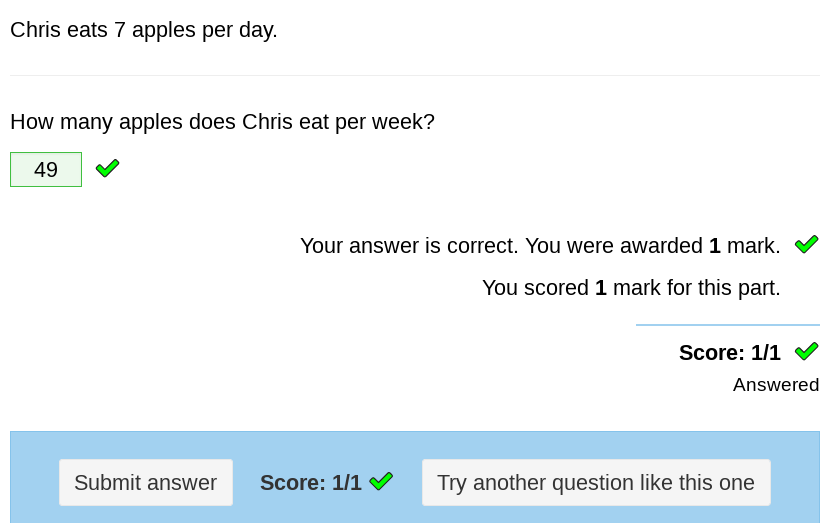
A preview of the question.

Variables

The question works. So what next?

The most important feature of computer-based assessment is the ability to dynamically generate questions which are different every time they are run. In Numbas this is achieved using variables.

Let’s change the question so that the number of apples eaten per day is picked at random. We do this by defining a variable in the Variables tab.

Click on the Add a variable button to add a new variable. Name it num_apples and select the data type Random number from a range. Choose numbers between 2 and 9 with step size 1.

Note

Why not include 1 in this range? Because then we’d have to think about whether to write ‘apple’ or ‘apples’ in the prompt. That’s a problem to solve later!

The description field gives you more space to describe what the variable represents. This will be useful when you come back to the question.

Write:

The number of apples eaten per day.

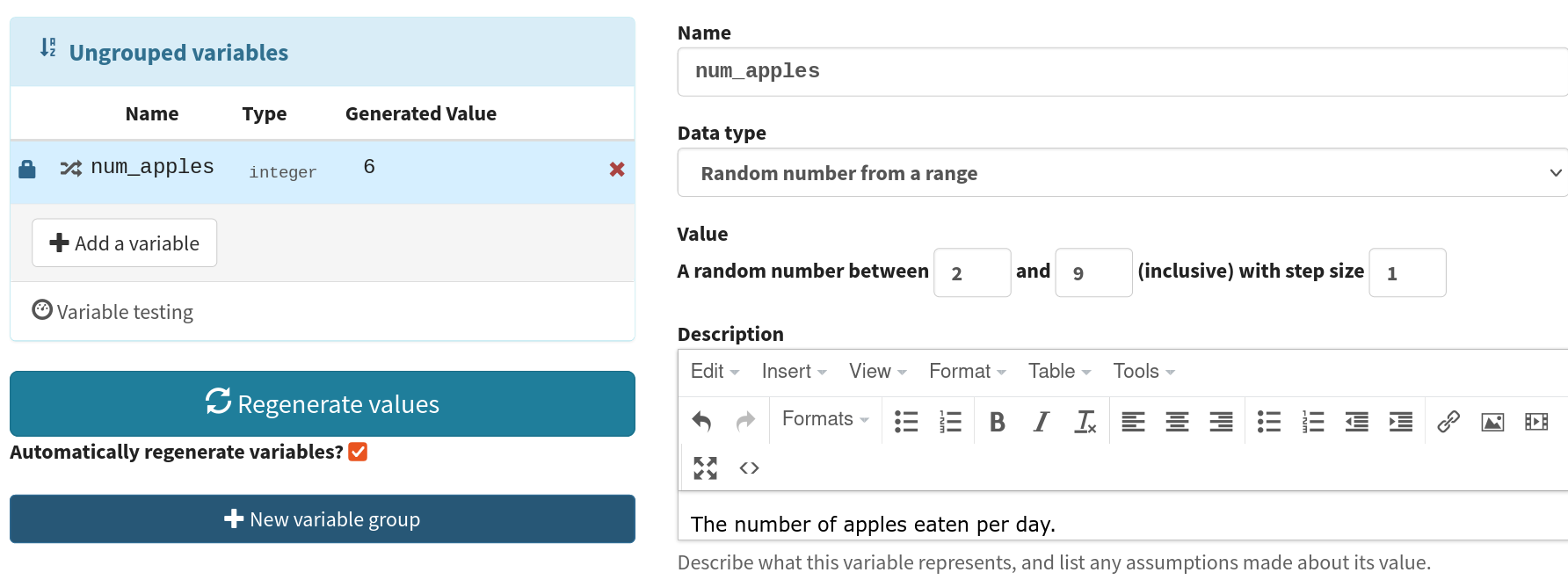
Defining the variable num_apples.

The Regenerate variables button on the left will give you a preview of the values that you can expect to be generated.

Now it’s time to replace the number 7 in the question with the new variable. Variables can be substituted in using curly braces: {}.

Click on Statement in the navigation bar, then change the statement to use the new variable:

Chris eats {num_apples} apples per day.

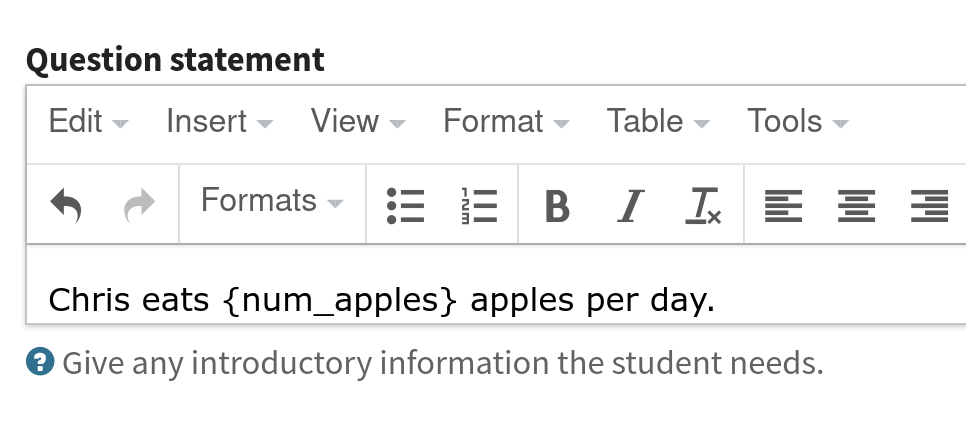
Using the variable in the question’s statement.

We also need to change the expected answer, which is currently hard-coded to 49. Click on Parts in the navigation bar, then go back to the Marking settings tab and change both minimum and maximum accepted value to 7 * num_apples.

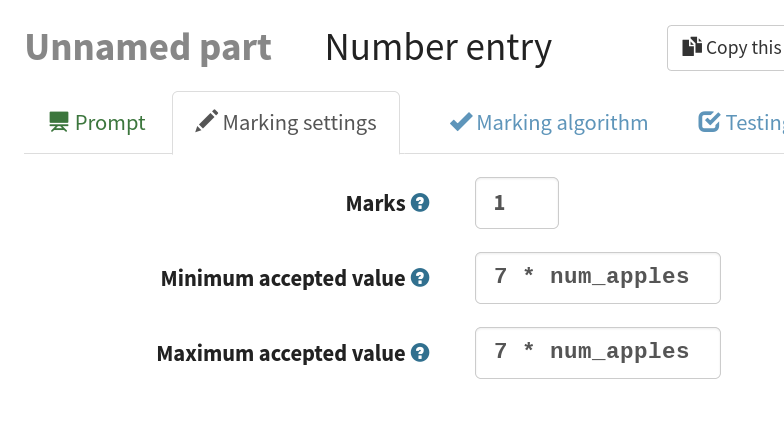
Calculating the answer based on the randomised variable.

When planning this question, we noted that the student might divide the number of apples by seven instead of multiplying. If the number of apples per day is not a multiple of seven, this will produce a fraction, which the student should be allowed to enter. Tick the Allow the student to enter a fraction? box.

Run your question again. You can click the Try another question like this one button to start the question afresh, with a new value of the random variable.

Advice

A question should provide a full solution to help students who get stuck or find the wrong answer.

Move to the Advice tab, and write:

Each day, Chris eats {num_apples} apples. There are 7 days in a week.

To find the number of apples Chris eats each week, multiply {num_apples} by 7.

Chris eats {7*num_apples} apples per week.

Now click Run again; if you press the Reveal answers button at the bottom of the question page, the number input is filled in with the correct answer, and the advice text you wrote is displayed at the bottom.

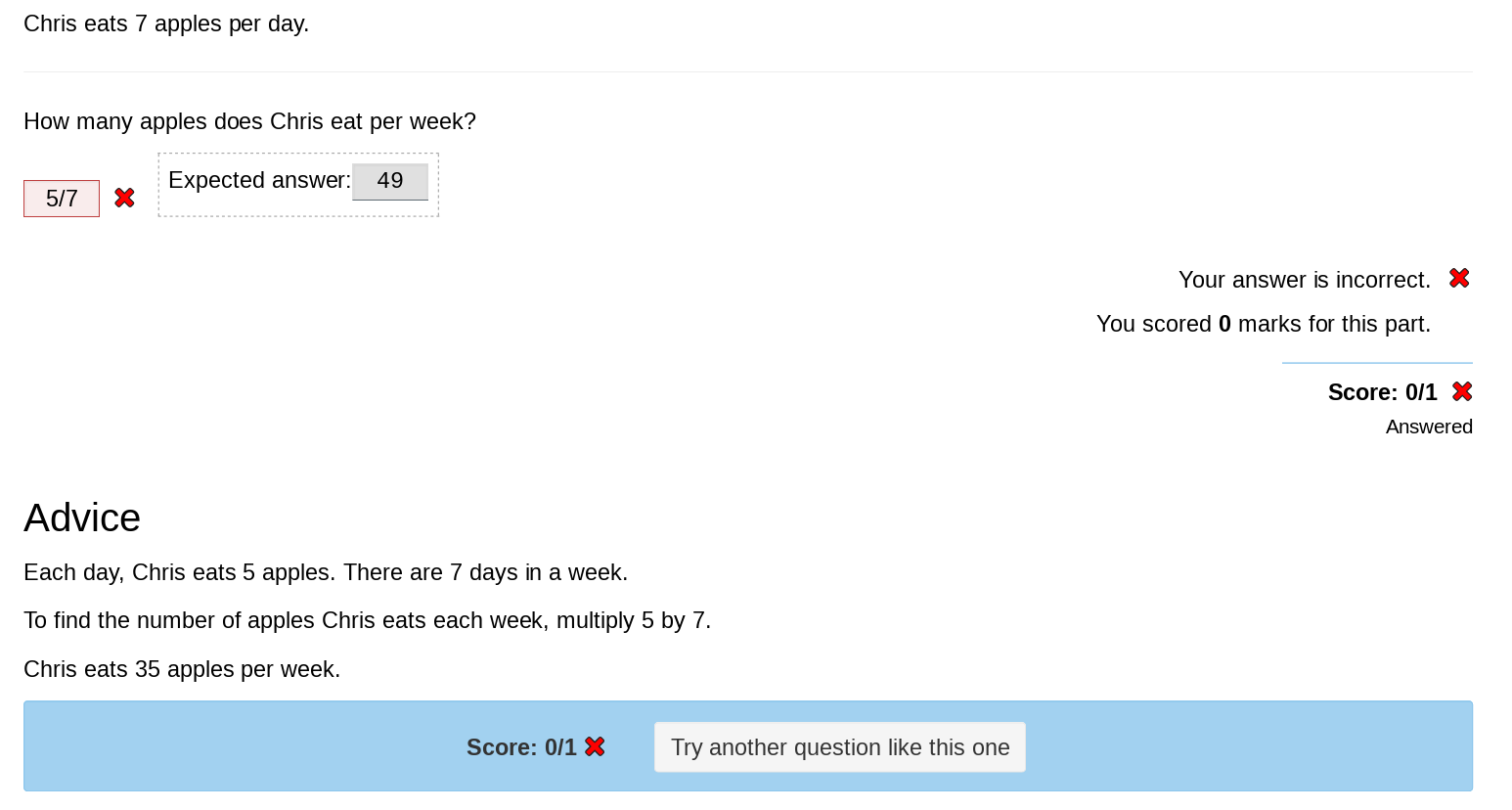
You have created your first complete question!